Расчет аннуитетных платежей по кредиту

Расчет аннуитетного платежа в Excel

Если вы планируете взять кредит, правильным будет заранее рассчитать платежи по нему. Так вы защитите себя от разочарований, когда в дальнейшем переплата по займу окажется слишком большой.

Рассчитать кредитные платежи можно не только на калькуляторе. Удобнее будет проводить такие вычисления на компьютере, ведь на каждом из них присутствует программа для работы с электронными таблицами Excel.

Теперь в ячейке автоматически появилась интересующая вас цифра

Обратите внимание, что это достаточно простые расчеты. Программа не требует никаких уточнений, но в реальном договоре нюансы могут быть прописаны. Так с помощью программы Excel вы можете самостоятельно в домашних условиях рассчитать ежемесячную сумму по аннуитетной схеме

А используя дополнительные функции программы, такие как ОСПЛТ и ПРПЛТ, можно рассчитать платежи по основному долгу и по процентам

Так с помощью программы Excel вы можете самостоятельно в домашних условиях рассчитать ежемесячную сумму по аннуитетной схеме. А используя дополнительные функции программы, такие как ОСПЛТ и ПРПЛТ, можно рассчитать платежи по основному долгу и по процентам.

График аннуитетных платежей прост и прозрачен. После нескольких оплат о нем можно и забыть. Если кредит стал для вас необходимостью, то такой вид кредитования будет удобным.

Расчет в Excel суммы кредита для заданного аннуитетного платежа

В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.

Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!

Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.

Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
• «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
• «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).

Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.

Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4)

Те самые параметры, которые мы вводили в таблице функции ПС.

Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:

• Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
• Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
• Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).

Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:

Скачать калькулятор расчёта суммы аннуитетного кредита в Excel

Досрочное погашение

Иногда появляется возможность внести большую сумму досрочно, независимо от графика. В таком случае необходимо явиться с паспортом и заявлением в банк. Но и здесь есть свои нюансы. Существует два вида досрочного погашения: полное досрочное погашение и частичное. Рассмотрим каждый из них.

Полное досрочное погашение подразумевает полное закрытие кредитного договора. При этом вносится вся оставшаяся сумма основного долга, но необходимо предупредить банк о таком намерении за 30 дней.

При полном досрочном погашении рассчитать сумму достаточно просто.

Для этого необходимо воспользоваться следующей формулой:

П = ОД + ОП

где:

• П – платеж;
• ОД – остаток суммы основного долга на дату внесения досрочного платежа;
• ОП – очередной платеж, ближайший к дате оплаты;

Возьмем для примера условия, приведенные выше. Допустим, 01.06.2015 года было принято решение закрыть кредитный договор. Для начала рассчитаем остаток основного долга, воспользовавшись графиком погашения из кредитного онлайн-калькулятора.

Дата	Всего	В погашение долга	В погашение процентов	Остаток после платежа
01.01.2014	5 287.11	3 287.11	2 000.00	96 712.89
01.02.2014	5 287.11	3 352.85	1 934.26	93 360.04
01.03.2014	5 287.11	3 419.91	1 867.20	89 940.13
01.04.2014	5 287.11	3 488.31	1 798.80	86 451.82
01.05.2014	5 287.11	3 558.07	1 729.04	82 893.75
01.06.2014	5 287.11	3 629.23	1 657.87	79 264.51
01.07.2014	5 287.11	3 701.82	1 585.29	75 562.69
01.08.2014	5 287.11	3 775.86	1 511.25	71 786.84
01.09.2014	5 287.11	3 851.37	1 435.74	67 935.47
01.10.2014	5 287.11	3 928.40	1 358.71	64 007.07
01.11.2014	5 287.11	4 006.97	1 280.14	60 000.10
01.12.2014	5 287.11	4 087.11	1 200.00	55 912.99
01.01.2015	5 287.11	4 168.85	1 118.26	51 744.14
01.02.2015	5 287.11	4 252.23	1 034.88	47 491.91
01.03.2015	5 287.11	4 337.27	949.84	43 154.64
01.04.2015	5 287.11	4 424.02	863.09	38 730.62
01.05.2015	5 287.11	4 512.50	774.61	34 218.13
01.06.2015	5 287.11	4 602.75	684.36	29 615.38
01.07.2015	5 287.11	4 694.80	592.31	24 920.58
01.08.2015	5 287.11	4 788.70	498.41	20 131.88
01.09.2015	5 287.11	4 884.47	402.64	15 247.41
01.10.2015	5 287.11	4 982.16	304.95	10 265.25
01.11.2015	5 287.11	5 081.80	205.30	5 183.44
01.12.2015	5 287.11	5 183.44	103.67	0.00
Всего заплачено	126 890.63	100 000.00	26 890.63

Подсчитав суммы платежей по основному долгу за последние шесть месяцев (с 01.07.2015г.), получаем сумму 29615,37 руб. подставляем в формулу:

П=29615,37+5287,11=34902,48

Итак, сумма полного досрочного погашения составит 34902,48.

Калькулятор по кредиту с нерегулярными оплатами

Все больше становятся популярными те виды займов, в договоре которых прописан пункт о возможности внесения нерегулярных оплат. Это удобно – человек в любую, выбранную им дату, перечисляет определенную, доступную для него, сумму. Конечно, ставка при таком соглашении будет на порядок выше, но зато свобода действий заемщика – больше. Это позволит погасить долг в более короткие сроки, перекрыв, тем самым, переплату по процентам.

Для того чтобы рассчитать схему внесения средств и отследить, когда кредит будет полностью погашен, подойдет более развернутая модель калькулятора. В программе Эксель такой сервис имеется. Это расширенная таблица, содержащая дополнительные графы, позволяющие рассчитать взносы с точностью не до месяца, как в стандартной модели, а за каждый день. Принцип получения результата следующий:

• первые два столбца таблицы зеленого цвета – это дата и сумма внесения. После перечисления платежа и добавления его размера в строке, расположенной под ней, появится отрицательное число – это и будет остаточная величина долга;
• следующие два столбца – тело кредита и проценты. Прописанные в них формулы, позволят наглядно увидеть, какая долговая часть пойдет на погашения самого займа, а какая покроет проценты;
• последний, пятый столбец – общий долг к выплате. Для удобства пользователя он окрашен в желтый цвет.
• Расчет полной стоимости ссуды с помощью Эксель

Порядок определения полной суммы долга – исходя из тела ссуды и переплаты по процентам, регламентирован действующим законодательством о потребительском кредитовании населения. Согласно нормативному документу при проведении исчислений используется формула:

ПСК = i х ЧБП х 100, где

• i – переплата по процентной ставке за базовый срок;
• ЧПБ – количество таких сроков в одном календарном году.

Базовый период рассчитывается следующим образом. По закону, это стандартные временные рамки, чаще всего фигурирующие в типовых банковских графиках погашения задолженностей. Большинство отечественных финансовых учреждений применяют 28 дневный срок. Таким образом, базовый период равен 28. Следовательно, ЧПБ = 365 (количество дней в году) : 28. Получаем 13. Примечательно, что этот показатель так же, в большинстве случаев, стандартный.

Теперь, имея на руках все необходимые цифры, можно подставлять их в формулу. Например, клиент берет в долг 400 000 рублей, сроком на 2 года (24 месяца), под ставку 22% годовых.

Выходит:

ПСК = 22/13 х 13 х 100 = 22%

Получаем, что при отсутствии дополнительных или скрытых комиссионных начислений, нередко устанавливаемых банками, ПСК полностью совпала с величиной ставки.

Чтобы узнать, сколько же всего необходимо отдать компании, чтобы кредит считался закрытым, нужно к размеру взятых денежных средств прибавить ПСК – в нашем случае, это 22%.

В этом видео подробно рассказано о том, как правильно подсчитать проценты по кредиту в таблице Эксель:

Таким образом, становится понятно, что пользоваться кредитным калькулятором в программе Excel достаточно просто, а преимуществ – масса. Основное из них – достоверность полученных данных, тогда как многие банки грешат тем, что калькуляторы, которые они предлагают на своих сайтах, содержат заведомо скрытые комиссии. Они автоматически увеличивают общую переплату и величину текущих взносов.

Расчет аннуитетных платежей по кредиту в Excel

В наш век высоких технологий и автоматизации как-то неприлично вручную выполнять сложные расчёты. Хоть аннуитетные платежи рассчитать не так и трудно, но как говорит Юрий Ашер:

«Не надо напрягать свой мозг там, где это могут сделать за вас другие!»

В нашей ситуации к вам на помощь придут: компьютер и программа Microsoft Excel.

Хотим предупредить, что команда портала temabiz.com поставила перед собой цель не просто дать вам «халяву» в виде «экселевского» файла с готовыми расчетами. Нет, в этой публикации мы вас научим самостоятельно рассчитывать аннуитетные платежи, а также составлять в программе Excel графики погашения аннуитетных кредитов. Ну а для ленивых мы, конечно же, выложим готовые файлы кредитных калькуляторов.

Задача1

1. Заемщик ежемесячно должен делать платеж банку. Этот платеж включает: сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов на остаток ссуды;
2. Сумма ежемесячного платежа (аннуитета) постоянна и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц;
3. Сумма для оплаты начисленных за прошедший период процентов уменьшается каждый период, т.к. проценты начисляются только на непогашенную часть ссуды;
4. Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды, увеличивается от месяца к месяцу.
5. Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
6. Проценты начисляются в конце каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода;
7. Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
8. В конце срока задолженность должна быть равна 0 (БС=0).

Решение1банкдалвозвращаем банку

Если процентная ставка = 0, то формула упростится до =(Пс + Бс)/Кпер Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:

Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А – это аннуитетный платеж (т.е. ПЛТ), К – это коэффициент аннуитета, а S – это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n – количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).

Таблица ежемесячных платежей

Составим таблицу ежемесячных платежей для вышерассмотренной задачи.

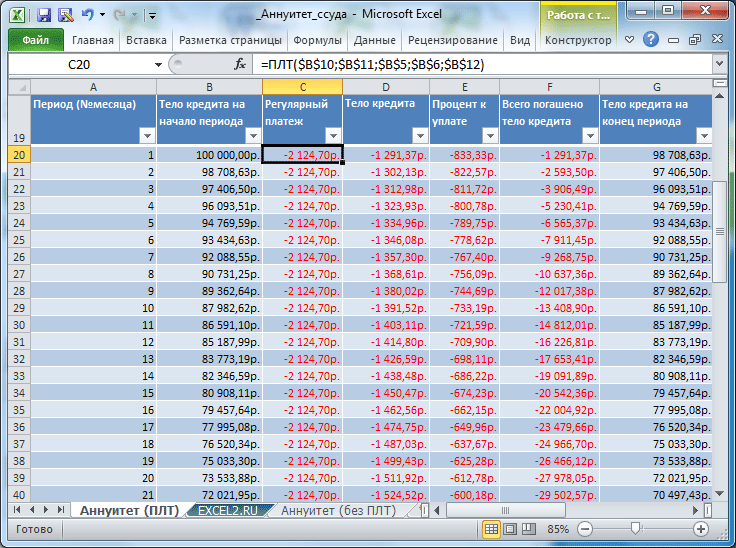
Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; ; ) практически с теми же аргументами, что и ПЛТ() (подробнее см. статью Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент период, который определяет к какому периоду относится сумма.

Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; ; ) с теми же аргументами, что и ОСПЛТ() (подробнее см. статью Аннуитет. Расчет в MS EXCEL выплаченных процентов за период).

Примечание. Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию ОБЩПЛАТ() , см. здесь.

Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо ПРПЛТ() или ОСПЛТ() , т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ

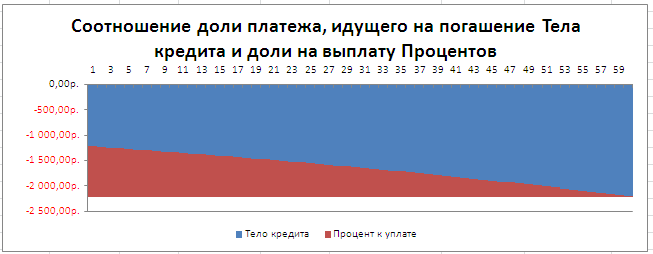
Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в файле примера .

Примечание. В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.

График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P файла примера лист Аннуитет (ПЛТ) , а также на листе Аннуитет (без ПЛТ) . Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см. файл примера лист Аннуитет (ПЛТ), столбцы H:I ).

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
2. Составим график погашения кредита. Пока пустой.
3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.

Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

Составим график погашения займа:

Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами — короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй — с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае — это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:

• «Ставка» — годовая процентная ставка по кредиту делённая на 12.
• «Кпер» — общий срок кредитования.
• «Пс» — сумма кредита (указывается со знаком минус).

Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» — координаты ячейки в которой вписывается сумма кредита (C4)

Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ»

По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение — эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12.
• «Кпер» – общий срок кредитования.
• «Пс» – сумма кредита (указывается со знаком минус).

Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус

Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках

Можно было просто вписать в строке формул то, что там сейчас вписано

По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:

Какую схему лучше выбрать

При ипотечном или автокредитовании клиенту не выгодны аннуитетные платежи. Что это значит? Клиент больше переплатит на процентах. В дифференцированной схеме тело кредита погашается равными частями. Одновременно уменьшается сумма процентов. Но есть обратная сторона медали. Сумма первых платежей может в разы отличаться от последних. Такие расходы может позволить себе далеко не каждый клиент. И банк это обязательно будет учитывать, рассчитывая лимит кредита. В зависимости от внутренних правил организации, ежемесячный платеж не должен превышать 20-25 % дохода. Если клиент хочет обслуживаться по дифференцированной схеме, у него должна быть высокая зарплата. Особенно если оформляется кредит на авто или ипотека. Аннуитетные платежи помогают планировать бюджет. Заемщик ежемесячно вносит одну и ту же сумму. Другое дело, что на первых этапах практически все деньги направляются на погашение процентов. Баланс меняется с середины срока. С другой стороны, такая схема будет выгодна предпринимателям, которые берут кредит на максимальную сумму для развития бизнеса и в ближайшее время планируют увеличить доход.

Особенности досрочного погашения кредита

1. Финансовая организация не вправе отказать заемщику в досрочном погашении кредита и эта возможность указана в статье 810 Гражданского кодекса РФ. Тем не менее банк необходимо уведомить о преждевременном внесении суммы не ранее чем за 30 дней, если в кредитном договоре не прописаны иные условия. В противном случае банк может отказать или пойти на встречу, но потребовать плату (комиссию) за внеплановое оказание услуг.
2. Большинство заемщиков думает, что погашение долга перед банком ранее запланированного срока всегда выгодно, однако это не так. Поскольку уровень инфляции в стране достаточно высокий, деньги со временем значительно обесцениваются и рубль сегодня, не равен рублю через 10-15 лет, таким образом инфляция зачастую «съедает» ставку по кредиту. Однако это утверждение актуально только для заемщиков со стабильной «белой» зарплатой, которая также индексируется из года в год.
3. Гасить кредит выгоднее многочисленными малыми суммами в первой половине срока, а не одной большой ближе к концу периода. Проценты выплачиваются в основном в начале срока и чем больше сумма остатка тем больше начисляется процентов, соответственно, чем позже начнут вносится средства в счет досрочки, тем незначительнее будет общая экономия.
4. Многократное преждевременное погашение разных кредитов, особенно в короткие сроки (через полгода-год после получения), может привести к снижению персонального рейтинга заемщика по причине ненадежности. Банку выгодно сотрудничество на длительный период, таким образом он обеспечивает себе постоянный и прогнозируемый денежный поток.
5. Досрочный платеж не всегда стоит вносить, как только появились лишние деньги. Некоторые банки учитывают преждевременные взносы меньше суммы ежемесячного долга в счет погашения процентов с соответственным снижением регулярного платежа в этом месяце. Рекомендуется уточнить подробности погашения в банке, вносить досрочку в день ежемесячного платежа или переводить сумму, превышающую этот платеж.
6. При долгосрочных кредитах и при наличии высокой вероятности их досрочного погашения необходимо оформлять страховку на каждый год отдельно, а не на весь срок сразу. В противном случае переплату за лишние месяцы/годы страхования беспроблемно смогут получить лишь заемщики с договорами от 1 сентября 2020 года, а все остальные только через суд.
7. Досрочное погашение кредита в счет уменьшения срока в большинстве случаев более выгодно по причине экономии на переплатах по процентам. Досрочное погашение в счет ежемесячного платежа удобно только при необходимости ослабления долгового бремени.

Используйте онлайн-калькулятор досрочного погашения, чтобы узнать на сколько уменьшится сумма ежемесячных платежей и срок кредитования при оплате кредита раньше установленного срока без визита в банк.

Кредитный калькулятор с досрочным погашением предоставлен сайтом calcus.ru

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

Таблица, составленная по условию задачи. В действительности можно задействовать другие столбцы для ее размещения

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом

Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

Таблица, составленная по условию задачи

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

Финальный результат. Практически двукратная переплата

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

Таблица, составленная по данным из условия задачи

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Окончательный результат расчета

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:

Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.